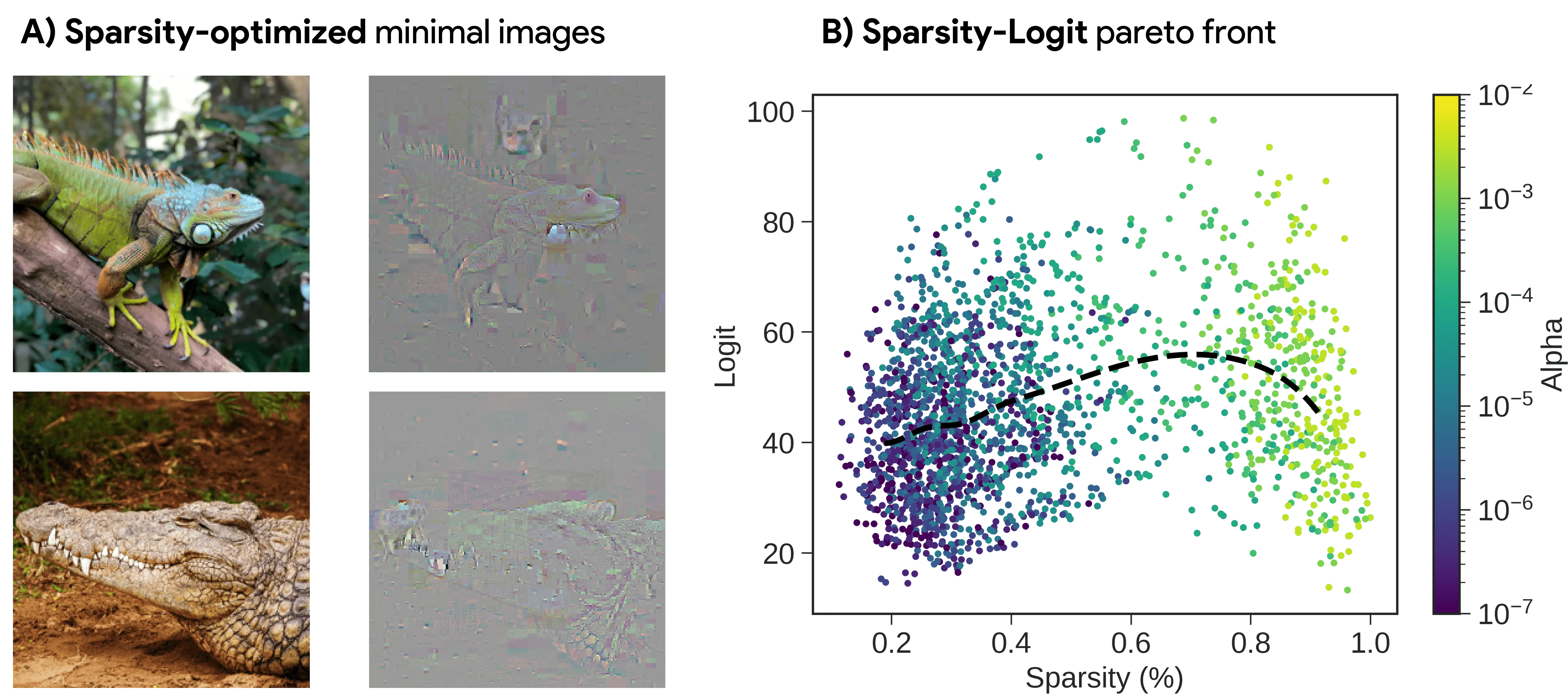
Bridging the gap with model robustness
In computer vision, several studies have observed a link between model robustness and a reliance on low-frequency image components (Zhang et al., 2022; Chen et al., 2022; Wang et al., 2020). This behavior has been demonstrated by filtering input images in the Fourier domain. However, since the Fourier transform discards spatial localization, these perturbations affect the entire image uniformly.
The Wavelet Attribution Method (WAM) offers a more structured alternative. In the wavelet domain, each scale corresponds to a dyadic frequency band with preserved spatial information. By summing the importance of wavelet coefficients at a given scale, WAM quantifies the model's reliance on specific frequency ranges. This provides a direct and interpretable estimation of spectral sensitivity—without requiring multiple perturbation passes or handcrafted filters.
To illustrate this property, we compare several ResNet models trained with different objectives: a standard ResNet (ERM) and three adversarially trained variants—ADV (Madry et al., 2018), ADV-Fast (Wong et al., 2020), and ADV-Free (Shafahi et al., 2019). For each model, we compute 1,000 explanations using WAM on ImageNet samples.
The figure below shows the average importance assigned to each wavelet scale. We normalize the explanations per image to highlight the relative use of fine versus coarse features. As expected, the vanilla ResNet relies more heavily on fine scales (high frequencies), whereas adversarially trained models shift attention toward coarser scales (lower frequencies).
This result confirms that WAM recovers known insights from the robustness literature and can be used to assess model sensitivity more efficiently. Indeed, WAM only requires a forward pass and therefore assessments a model's or a prediction robustness can be made on-the-fly.
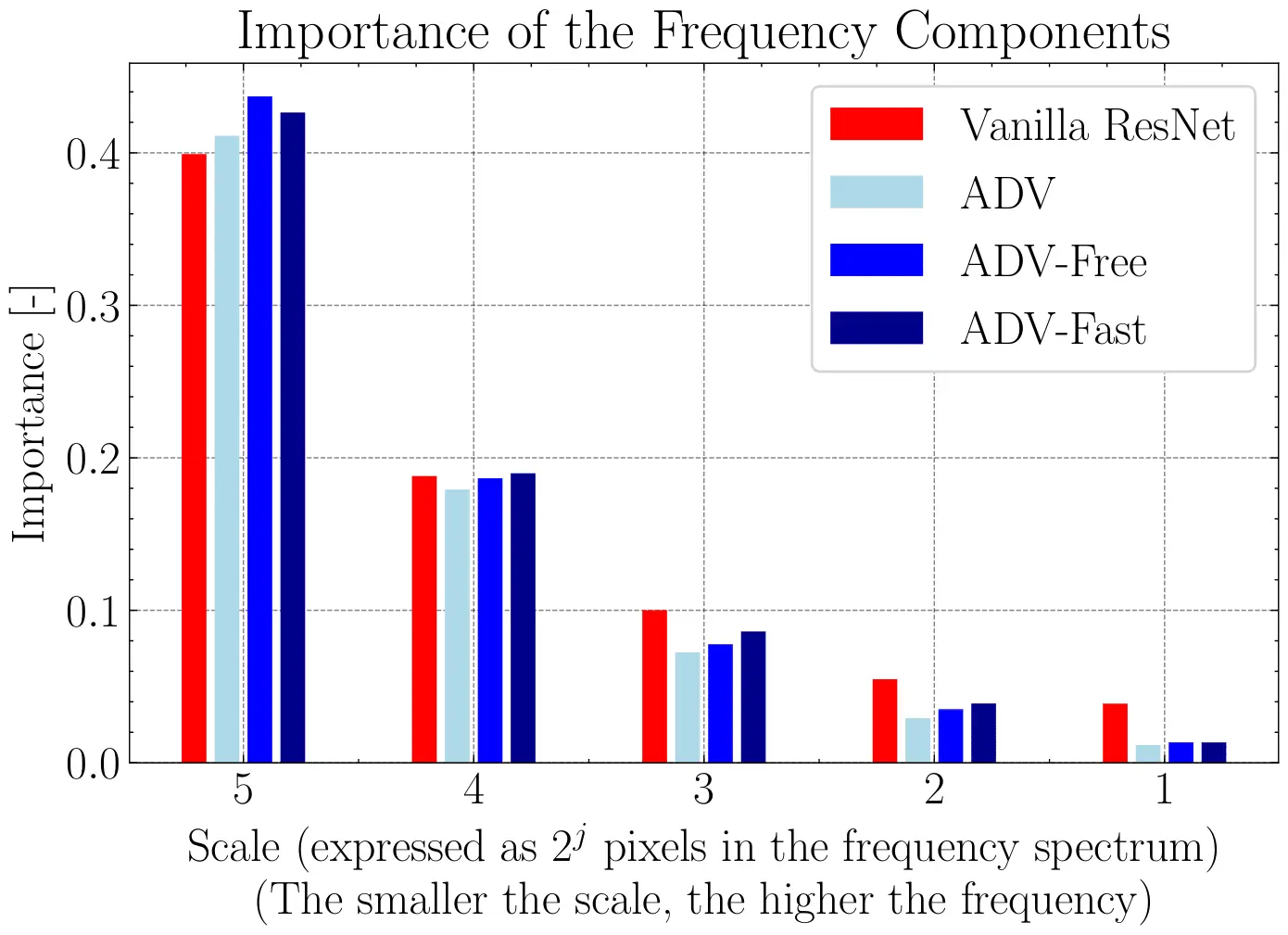
Model robustness assessment with WAM. Each bar shows the relative importance of each wavelet scale in the model’s prediction. Explanations are averaged over 1,000 ImageNet images and normalized per sample. Adversarially trained models shift attention toward coarser (low-frequency) features, confirming robustness patterns documented in prior work.