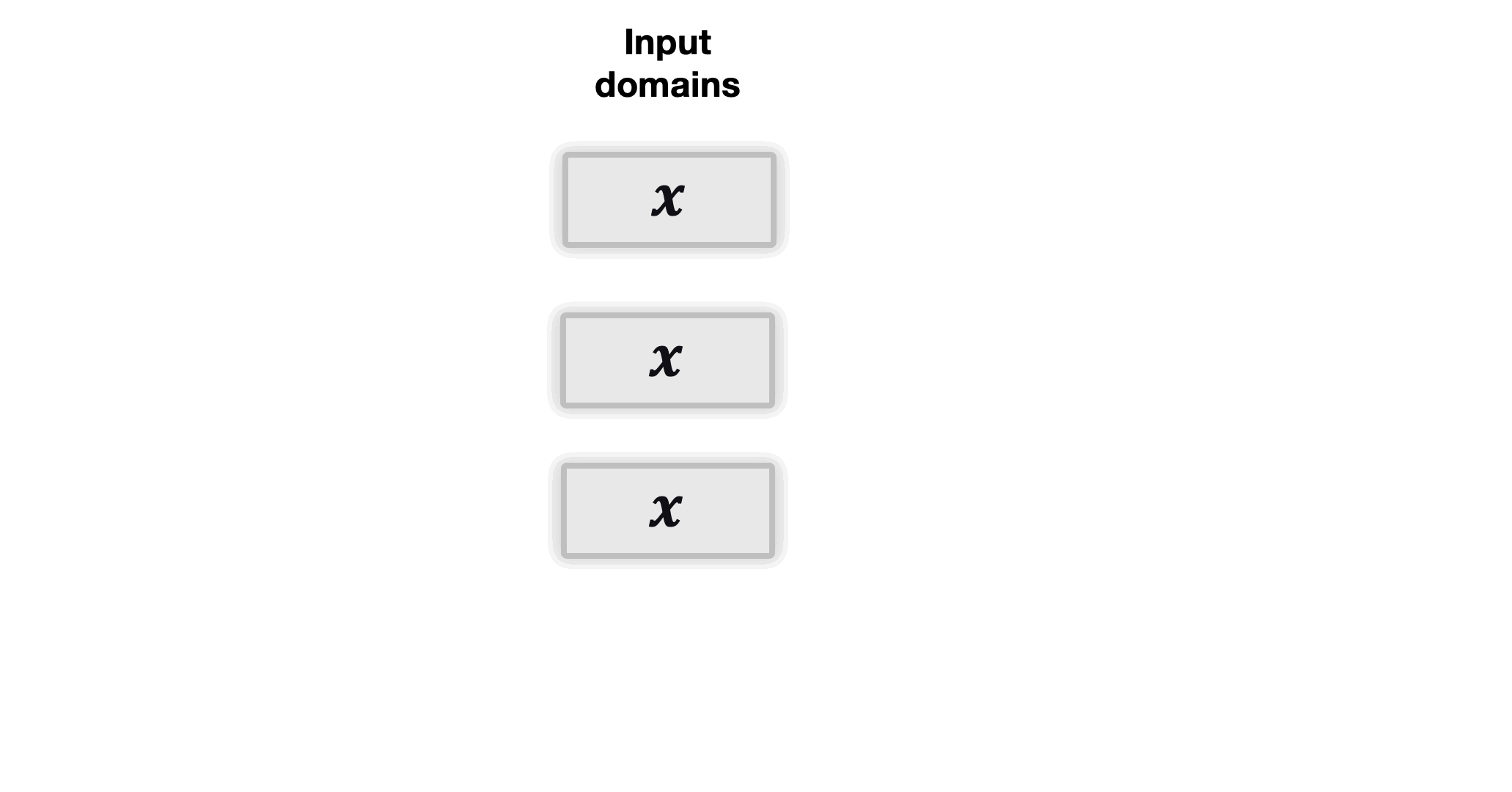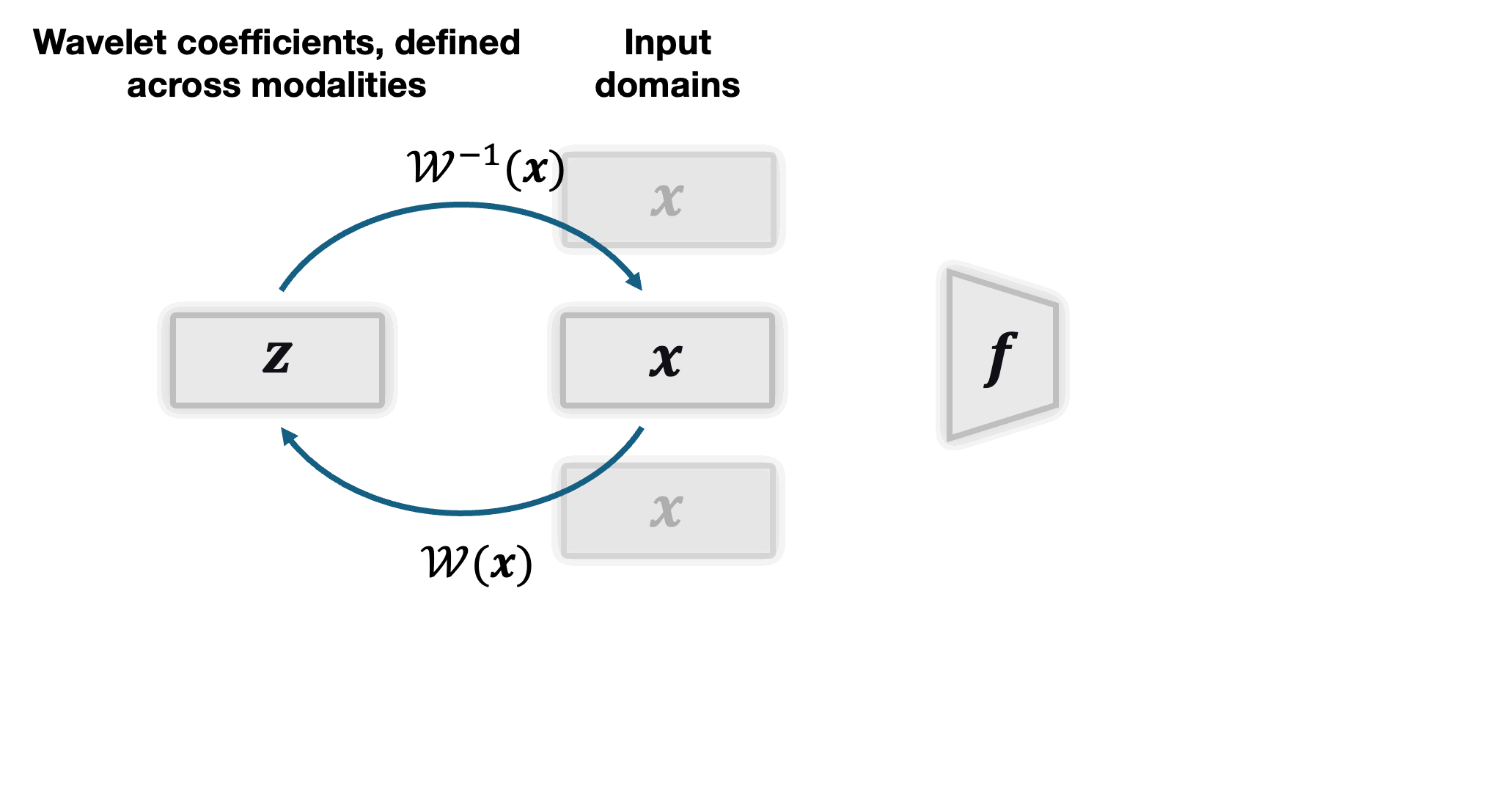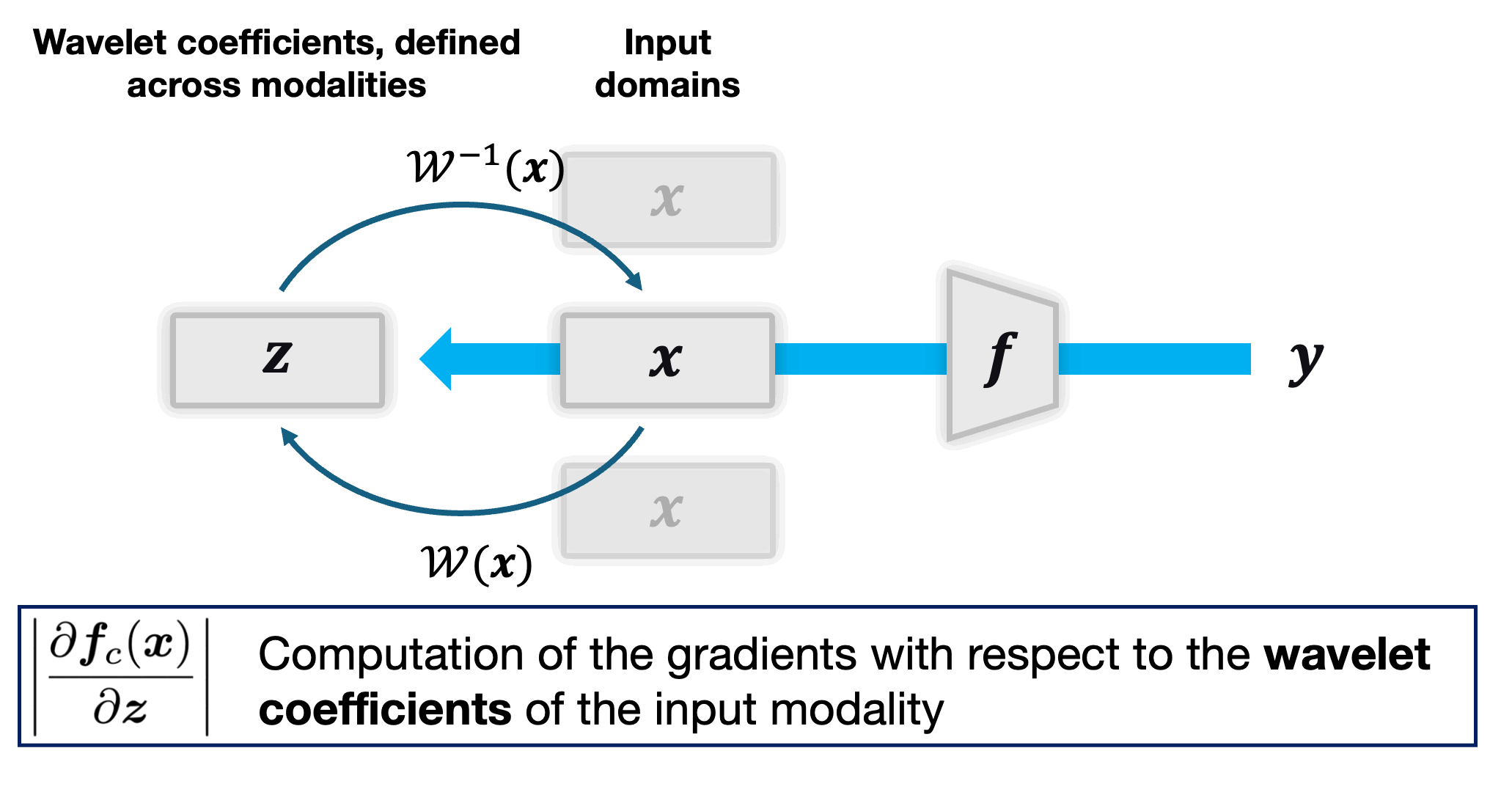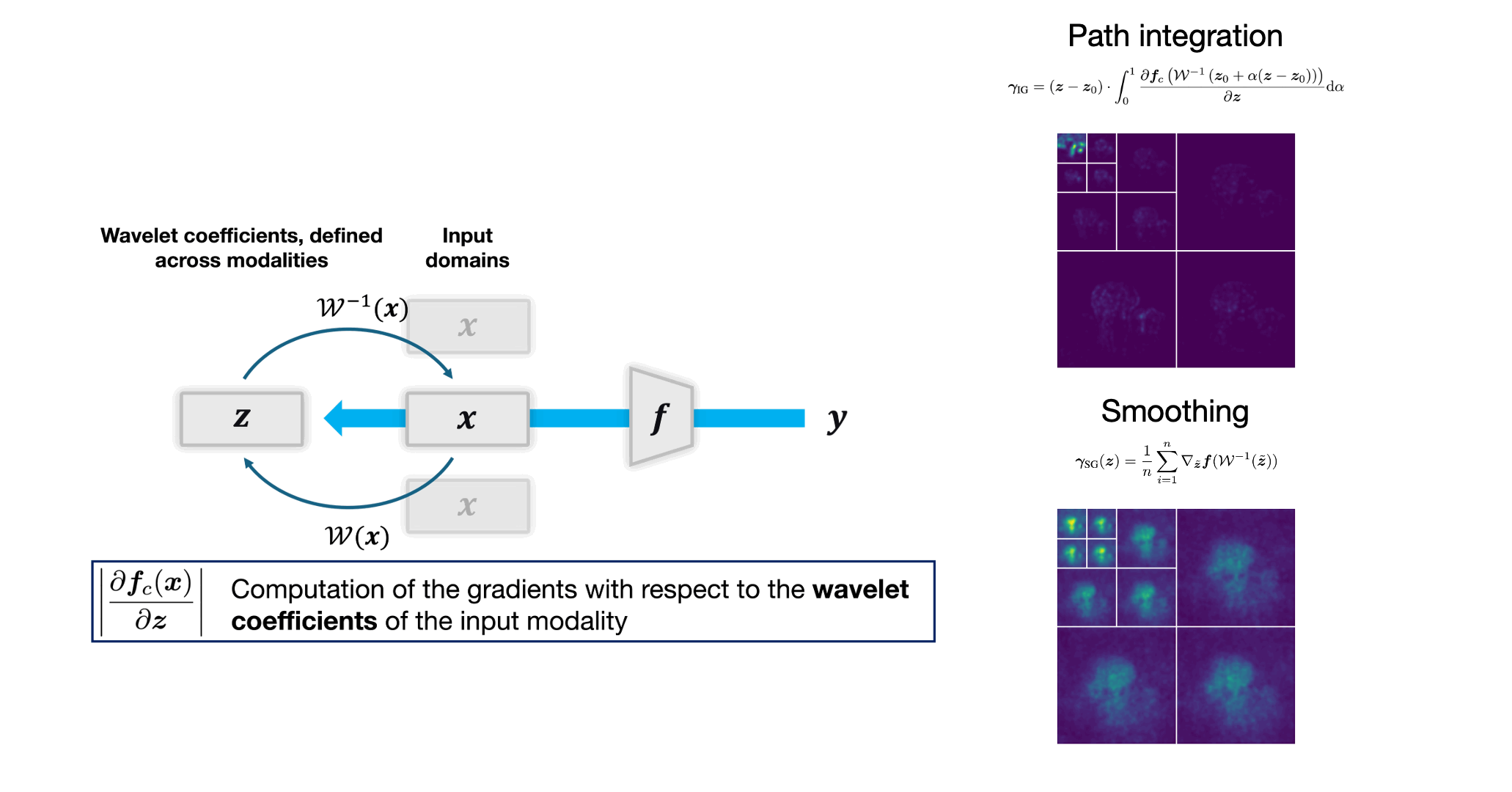
Multiscale decompositions
Wavelets decompose signals into components that retain both spatial and frequency information, unlike Fourier transforms, which capture only frequency and discard spatial or temporal context. The choice of the wavelet determines what kind of structural components will be highlighted on the image. Its choice is therefore grounded in the application at hand.
A wavelet is a function $\psi \in \mathcal{H} = L^2(\mathbb{R}^n)$ that is normalized, centered at the origin, and has zero mean, i.e., $\int_{\mathbb{R}^n} \psi(x) \, dx = 0$. This function $\psi$ is called the mother wavelet, and it serves as the building block for constructing a family of wavelets via scaling and translation.
$$\psi_{\lambda,b}(x) = \frac{1}{\lambda^{n/2}} \, \psi\left(\frac{x - b}{\lambda} \right) \tag{1}$$
To analyze signals using wavelets, we often discretize the scale and translation parameters. A common and efficient choice is to use dyadic scales $\lambda = 2^j$ and translations on a dyadic grid $b = 2^j k$, where $j, k \in \mathbb{Z}$. This leads to the Discrete Wavelet Transform (DWT), based on the countable family:
$$\left\{ \psi_{j,k}(x) = 2^{j n/2}\, \psi\!\left(2^{j} x - k \right) \right\}_{j,k \in \mathbb{Z}} \tag{2}$$
The DWT represents a signal $g \in L^2(\mathbb{R}^n)$ by projecting it onto this family. The wavelet coefficients are obtained as inner products:
$$\mathcal{W}_{\mathrm{DWT}}(g)(j,k) = \langle g, \psi_{j,k} \rangle = \int_{\mathbb{R}^{n}} g(x)\,\overline{\psi_{j,k}(x)} \, dx \tag{3}$$
These coefficients measure the content of $g$ at scale $2^{-j}$ and location $2^{-j}k$. When $\psi$ satisfies certain admissibility and regularity conditions, the DWT becomes an invertible transform, and the signal can be exactly reconstructed:
$$\forall x\in\mathbb{R}^n,\quad g(x) = \sum_{\substack{j \in \mathbb{Z} \\ k \in \mathbb{Z}^n}} \langle g, \psi_{j,k} \rangle\psi_{j,k}(x), \tag{4}$$
where $\mathcal{W}_{\mathrm{DWT}}(g)(j,k)=\langle g, \psi_{j,k} \rangle$.
The figure below illustrates the process of decomposing an input image into its wavelet components.

Computation of the dyadic wavelet transform. A mother wavelet $\psi$ convoluted with the original image at different orientations to obtain the horizontal, vertical, and diagonal components at a given scale. The process is repeated for each scale, resulting in a multiscale decomposition of the image.
The multiscale and localized nature of the wavelet transform allows for the analysis of both fine and coarse features, making it especially powerful for signals with hierarchical or spatially varying content.
The selection of the mother wavelet $\psi$ depends on the application. Haar wavelets are well-suited for detecting sharp discontinuities, while smoother wavelets like Daubechies are better for representing gradual transitions.
In practice, the choice is guided by the characteristics of the data and the goals of the analysis. For image processing, wavelets that are localized in both space and frequency and have directional sensitivity are often preferred. The interpretability and effectiveness of the wavelet decomposition are directly linked to how well the chosen $\psi$ matches the underlying structures in the data.